뉴턴의 점성 법칙 (Newton’s law of viscosity)
뉴턴의 점성 법칙 (Newton’s law of viscosity)
정의
예를 들어 아래 그림과 같이 아래 판(빨간색 boundary plate)이 고정된 상태에서 위쪽의 파란색 판 (파란색 boundary plate)이 속도 u로 움직인다고 생각해보자. 아래 판에서의 유체의 속도는 0이 되고 위판에서의 유체의 속도는 u가 된다. 그 사이에 유체속도는 검은색 화살표와 같이 되며 판을 움직이기 위한 단위 면적당 힘 (전단 응력) 을 τ라고 하자.
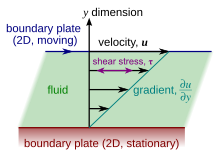
( 실제 속도 구배 는 직선은 아니고 아래 그림처럼 곡선의 형태이다. )

뉴턴의 점성법칙 수식
- τ : 전단 응력 (shear stress)
- μ : 점성계수 (viscosity); 압력 및 온도의 함수
: 전단 변형율
위와 같이 전단 변형율이 전단 응력에 정비례하는 유체를 뉴턴 유체 (Newtonian fluid) 라고 한다. 우리가 일반적으로 알고 있는 물이나 공기와 같은 것이 뉴턴 유체이다. 아래 그림에서 왼쪽이 점성계수가 작고 오른쪽이 점성계수가 큰 유체이다.

비뉴턴 유체 (Non-newtonian fluid)
(압력과 온도가 일정할 경우) 뉴턴 유체는 점성계수가 상수인데 반해 속도구배에 따라 변하는 점성계수를 가지는 경우에 비뉴턴 유체 (Non-newtonian fluid) 라고 한다.
대표적인 예로 벌꿀, 치약, 피, 샴푸 같은 것이 있다. 아래 그림을 보면 뉴턴 유체는 기울기가 일정한 직선형태 (파란색선) 이지만 비뉴턴 유체 (검은색 선)는 그렇지 않다.

점성계수의 단위 및 차원
τ 의 단위 (응력이므로 단위 면적당 힘) : N/m^2
y 의 단위 : m
v 의 단위 : m/s
이므로
점성계수의 단위는 N/m^2 x m x s/m = N s / m^2 = Pa s
점성계수의 차원은 N s^2 / m^2 -> F L^-2 T
아래는 물의 점성계수의 예이다.
| Temperature (°C) | Viscosity (mPa·s) |
|---|---|
| 10 | 1.3059 |
| 20 | 1.0016 |
| 30 | 0.79722 |
| 50 | 0.54652 |
| 70 | 0.40355 |
| 90 | 0.31417 |
동점성 계수 (kinematic viscosity)
동점성 계수는 점성계수를 밀도로 나눈값이다.
동점성계수의 단위는 (N s / m^2) / (kg / m^3) = m^2 / s
* F=ma 를 이용하면 N 단위 => kg m / s^2 단위와 같다.
동성계수의 차원은 m^2 / s-> L^2 T^-1
표준 대기압 ( 25 도씨, 1 bar )에서 공기의 동점성 계수는 18.5 μPa·s 이며 대략 동일 온도의 물보다 약 50배 정도 작다.
참고문헌
https://en.wikipedia.org/wiki/Non-Newtonian_fluid
https://en.wikipedia.org/wiki/Newtonian_fluid
https://en.wikipedia.org/wiki/Viscosity