카르노 싸이클 (Carnot cycle)
카르노 싸이클 (Carnot cycle)
카르노라는 아저씨가 제안한 이론적인 (이상적인) 싸이클이다.
이 싸이클의 효율은 열역학적 엔진 효율의 최고점이 된다 (=어떠한 엔진도 이보다 효율이 좋을 순 없다).
프로세스
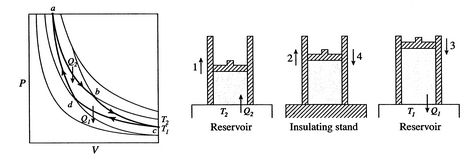
* T2 > T1
4개의 프로세스 (두개의 단열 가역 + 두개의 등온 가역) 로 구성된다.
위 오른쪽 그림은 카르노 싸이클을 열탱크가 붙어있는 피스톤 (내부에는 이상기체) 에 적용한 그림이다.
a -> b -> c -> d
1. 등온 과정 (온도 T2, Q2 > 0) : a -> b
열탱크로부터 피스톤으로 열 Q2가 전달되는 과정에서 내부 기체의 온도가 일정하게 T2으로 유지되며 압력이 감소하고 부피는 증가하는 과정
2. 단열 과정 (Q=0) : b (T2) -> c (T1)
열적으로 차단된 상태 (단열) 에서 온도가 낮아지면서 압력이 낮아지고 부피는 팽창하는 과정
(위의 등온 과정과 달리 열이 공급되지 않는 단열 과정이며 온도가 낮아지게 된다.)
3. 등온 과정 (온도 T1, Q1 < 0) : c -> d
열탱크로 열이 유출되는 과정에서 내부 기체의 온도가 일정하게 T1으로 유지되며 압력이 증가하고 부피는 감소하는 과정
(위의 1. 등온 과정의 역과정)
4. 단열 과정 (Q=0) : d (T1) -> a (T2)
열적으로 차단된 상태 (단열) 에서 온도가 높아지면서 압력이 증가하고 부피는 감소하는 과정
(위의 2. 단열 과정의 역과정)
효율

* 위 식의 유도 과정
열적 효율식 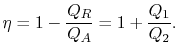 에서
에서
![]()
![]()
을 적용하면
![$\displaystyle \eta = 1+ \frac{T_1[\ln(V_d /V_c)]}{T_2[\ln(V_b /V_a)]}.$](https://web.mit.edu/16.unified/www/FALL/thermodynamics/notes/img355.png)
단열 가역 과정식 ![]() 혹은
혹은 ![]() 를 적용하면
를 적용하면

위의 두 효율식과 위 부피식을 연계하면 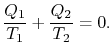
결과적으로 위식을 처음 열적 효율식에 대입하면 
참고문헌
https://web.mit.edu/16.unified/www/FALL/thermodynamics/notes/node24.html
https://en.wikipedia.org/wiki/Carnot_cycle