
진동 이론 - 자유 진동 (free vibration)
(기계공학에서 진동의 이론적인 배경에 대하여)

위와 같은 1 자유도 (DOF, degree of freedom) 시스템의 자유 진동 (free vibration)의 운동 방정식은 아래와 같다.
(보통 아래와 같이 미분 방정식으로 표현된다.)
여기서
m : 질량
c : 감쇠
k : 강성
x : 변위
: 속도 (변위를 시간에 대하여 미분하면 속도가 된다)
: 가속도 (변위를 시간에 대하여 두번 미분하면 가속도가 된다)
자유 진동은 외력이 없이 물체 혼자 진동할 때의 움직임을 나타낸다.
( 우측의 0 대신에 다른 항이 있으면 강제 진동 방정식이 된다.)
첫번째항은 우리가 잘 아는 뉴턴 형님의 관성의 법칙 (F=ma)에서 나온 관성력이다.
세번째항은 우리가 잘 아는 스프링의 힘 (F=kx, 후크의 법칙) 이다.
두번째항은 감쇠력으로 물체의 속도에 비례하는 항이다.
문위에 문이 꽝하고 닫히지 않게 댐퍼가 달려 있는 것을 볼 수 있는데 문을 빨리 닫을때 더 힘을 많이 써야한다.
두번째 항이 있는 경우는 감쇠 진동 (damped vibration) 이고 없으면 비감쇠 진동 (undamped vibration) 이다.
비감쇠 진동 (undamped vibration)
진폭의 감소 없이 진동한다.
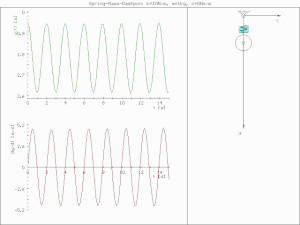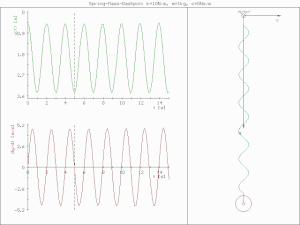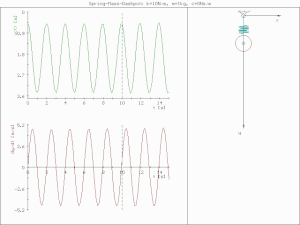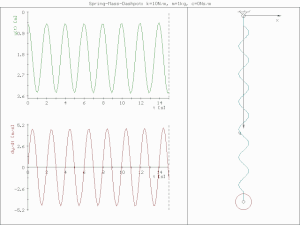
비감쇠 진동의 운동 방정식은 감쇠가 없으므로 (c=0) 아래와 같이 표현된다.
고유 진동수는 간단한 과정을 거쳐 아래와 같이 표현된다.
즉 비감쇠 고유 진동수 (undamped natural frequency) 는
그냥 고유 진동수라고도 한다. 중요한 수식이니 꼭 외우자.
감쇠 진동 (damped vibration)
감쇠 진동은 감쇠값에 따라 또 다시 3가지도 나누어진다.
는 critical damping 이라고 하며 질량과 강성으로 결정되는 특정 감쇠값이다.
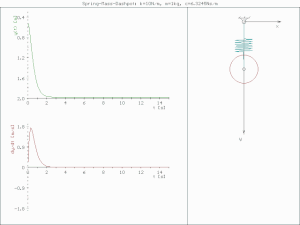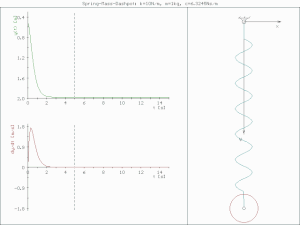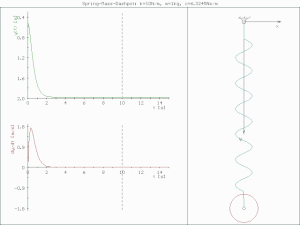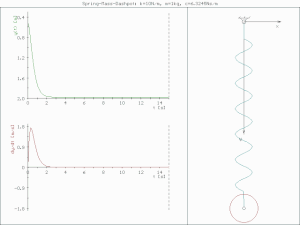
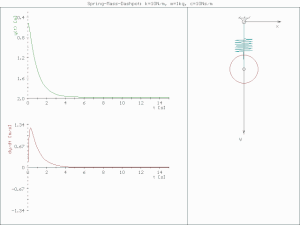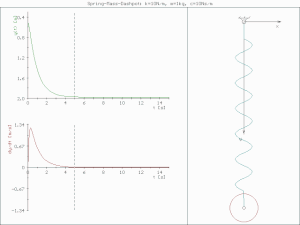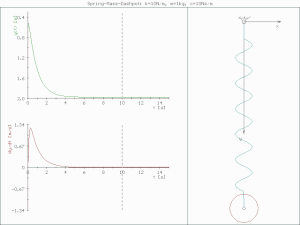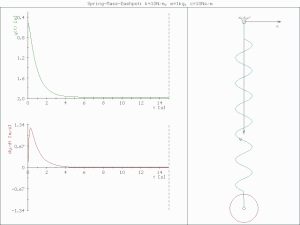
underdamped (c < )
진폭이 점점 줄어들며 진동한다.
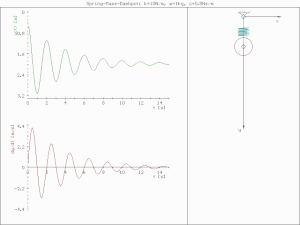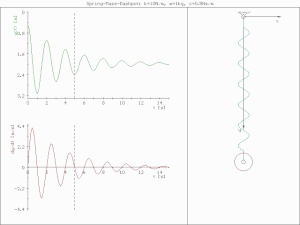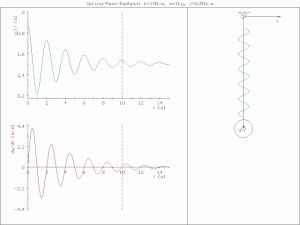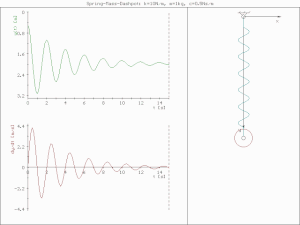
critically damped (c= )
더이상 진동하지 않게 되는 감쇠값
overdamped (c > )
여기서도 더 진동하지 않는다.
감쇠비 (damping ratio)
로 보통 표시하며 critical damping 대비 실제 감쇠의 비율이다. 감쇠비가 1이되면 critically damped 진동을 하게 된다. 1보다 크면 overdamped 가 되고 1보다 작으면 underdamped 가 된다.
예를 들어 비행기 연료탱크, 엔진 크랭크 샤프트와 같은 금속 구조물은 보통 감쇠비가 0.05 이하이며 자동차 서스펜션 처럼 의도적으로 감쇠를 크게하는 구조물은 0.2~0.3 정도가 된다.
감쇠 진동의 고유 진동수 (damped natural frequency)
감쇠 진동의 고유 진동수는
비감쇠 진동의 고유 진동수에 비해 작다. 그러나 대부분의 시스템에서 감쇠비가 작아 거의 비슷하다.
'이론' 카테고리의 다른 글
| 압력의 단위 (0) | 2018.12.26 |
|---|---|
| fast Fourier transform (FFT) (1) | 2018.12.24 |
| 주파수 (frequency) (3) | 2018.11.30 |
| 폰 미세스 등가 응력 (von Mises equivalent stress) (0) | 2018.07.02 |
| 평면 응력과 평면 변형율 (0) | 2017.04.21 |






