단면 1차 모멘트
단면 1차 모멘트 (면적 1차 모멘트) 의 영어로 first moment of area 이며 first moment of inertia로 잘못 불리는 경우도 많다.
단면적에 대한 특성값으로 면적에 길이를 곱한 것을 더한 (적분한) 값으로 단위는 길이의 세제곱이 된다. (예를 들어 m^3 혹은 mm^3)
공식은 간단하다. 아래 수식을 보면 알겠지만 x, y, dA 의 함수이며 이는 단면 1차 모멘트가 형상만의 함수라는 것을 의미한다. 즉 형상이 결정되면 단면 1차 모멘트가 결정되는 것이다.
도심 (Centroid)
어떠한 형상에 대한 도심의 정의는 모든 점의 산술 평균 (arithmetic mean) 위치를 의미한다.
수식적으로는 아래와 같이 된다. 눈치가 없는 사람도 알겠지만 위 단면1차 모멘트식과 같다.
-> 즉, 단면 1차 모멘트가 0이 되는 점이 도심이 된다.
( 물리적으로는 밀도가 균일한 경우에 도심은 무게중심과 같게 된다. 즉 이점에 실을 연결하여 들면 기울어지지 않는다.)
미리 구해놓은 도심들
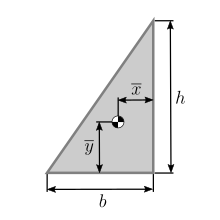
삼각형
=
,
=
사각형
=
,
=

사분원
=
,
=

반원
= 0,
=

참고 사이트
위의 공식을 간단한 단면적에 대해서는 이미 구해 놓은 값들이 있다.
https://mechanicalc.com/reference/cross-sections
중심 축에서 떨어져 있는 경우 구하는 방법을 정리해 놓은 싸이트도 있다.
https://skyciv.com/tutorials/calculating-statical-or-first-moment-of-area-of-beam-sections/
'이론' 카테고리의 다른 글
| 후크의 법칙 (Hook's law) (1) | 2019.01.03 |
|---|---|
| 모어의 원 (Mohr's circle) (1) | 2019.01.03 |
| 포아송 비 (Poisson's ratio) (0) | 2018.12.27 |
| 변위, 속도, 가속도 관계 (2) | 2018.12.26 |
| 압력의 단위 (0) | 2018.12.26 |










