모어의 원 (Mohr's circle)

2019. 1. 3. 10:30

모어의 원 (Mohr's circle)

쉽게 말해 응력의 좌표 변환을 해주는 원이다. 크리스티안 오토 모어님께서 만드셨다.

하중을 받는 구조물의 한점의 응력은 좌표축에 따라 응력의 성분이 달라진다.

(응력 자체가 바뀌는 것은 아니고 어느 축에서 보는냐에 따라서 응력의 성분이 달라진다. 잘 이해가 가지 않는다면 힘 벡터를 어느 좌표축으로 분석을 하느냐에 따라 성분이 달라진다고 보면 된다.)

아래 그림은 3차원 좌표에서의 응력 상태를 나타내는 모어의 원이다.

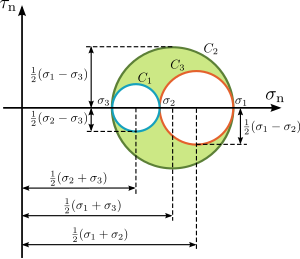
아래와 같이 3차원에서는 한점은 9개의 응력 스칼라량을 가진다. 이러한 것을 코시 응력 텐서 (Cauchy stress tensor) 라 한다.

${\boldsymbol {\sigma }}=\left[{{\begin{matrix}\sigma _{{11}}&\sigma _{{12}}&\sigma _{{13}}\\\sigma _{{21}}&\sigma _{{22}}&\sigma _{{23}}\\\sigma _{{31}}&\sigma _{{32}}&\sigma _{{33}}\\\end{matrix}}}\right]\equiv \left[{{\begin{matrix}\sigma _{{xx}}&\sigma _{{xy}}&\sigma _{{xz}}\\\sigma _{{yx}}&\sigma _{{yy}}&\sigma _{{yz}}\\\sigma _{{zx}}&\sigma _{{zy}}&\sigma _{{zz}}\\\end{matrix}}}\right]\equiv \left[{{\begin{matrix}\sigma _{x}&\tau _{{xy}}&\tau _{{xz}}\\\tau _{{yx}}&\sigma _{y}&\tau _{{yz}}\\\tau _{{zx}}&\tau _{{zy}}&\sigma _{z}\\\end{matrix}}}\right]$

2차원 응력 상태의 모어의 원

대부분 이해를 돕기 위해서 3차원 문제가 아닌 간단화된 2차원 응력 상태의 모어의 원을 다룬다 (모두가 3차원은 어렵다고 생각했기 때문이지...).

아래와 같이 2차원 평면 응력 상태 를 가정하면 3개의 응력 성분만 남게 된다.

${\boldsymbol {\sigma }}=\left[{{\begin{matrix}\sigma _{x}&\tau _{{xy}}&0\\\tau _{{xy}}&\sigma _{y}&0\\0&0&0\\\end{matrix}}}\right]\equiv \left[{{\begin{matrix}\sigma _{x}&\tau _{{xy}}\\\tau _{{xy}}&\sigma _{y}\\\end{matrix}}}\right]$

주 응력과 주 축

아래 그림에서 보면 한 점의 응력 상태는 정의되는 좌표축에 따라 A~E 로 모두 표현될 수 있으며

(즉 어느 축에서 정의하냐에 따라 응력값이 달라지는 것이다. 예를 들어 AB 축에서 보면 응력의 상태는 A상태의 값이 나오고 EC 축에서 보면 응력의 상태는 전단응력이 0인 E 상태의 값이 나오기도 한다.)

특히 C 점과 E 점은 전단응력 tau가 0이 되는 지점으로 이때의 응력 sigma1과 sigma2는 주 응력 (principal stress) 이라고 하며 이때의 좌표축을 주 축 (principal axes) 한다.

모어의 원 사용법

모어의 원은 한점의 응력상태 (예를 들어 위 그림에서 A 점) 을 알면 모어의 원을 그릴 수 있고 이 원을 통해 어느 좌표에서도 응력 값을 (예를 들어 C, D, E 점)의 응력 상태를 구할 수 있는 것이다. 이는 곧 주축과 주응력도 구할 수 있다는 말이다.

예제

잘 이해가 안갈테니 예제나 풀어보자.

$\sigma _{{x'}}=-10{\textrm {MPa}}$

$\sigma _{{y'}}=50{\textrm {MPa}}$

$\tau _{{x'y'}}=40{\textrm {MPa}}$

어느 점의 응력 상태가 위와 같을 때 모어의 원을 이용해서 주응력과 주축을 구하라.

아래 식은 복잡해 보이지만 원리를 이해하면 간단하다 (공식같은 걸 미리 외울 필요없이 그냥 쉽게 풀 수 있다!!!)

아래는 피타고라스 정리를 이용해서 모어원의 반경을 구하는 식

${\begin{aligned}R&={\sqrt {\left[{\tfrac {1}{2}}(\sigma _{x}-\sigma _{y})\right]^{2}+\tau _{{xy}}^{2}}}\\&={\sqrt {\left[{\tfrac {1}{2}}(-10-50)\right]^{2}+40^{2}}}\\&=50{\textrm {MPa}}\\\end{aligned}}$

아래는 모어원의 중심을 구하는 식

${\begin{aligned}\sigma _{{\mathrm {avg}}}&={\tfrac {1}{2}}(\sigma _{x}+\sigma _{y})\\&={\tfrac {1}{2}}(-10+50)\\&=20{\textrm {MPa}}\\\end{aligned}}$

이로서 모어의 원은 구해졌다.

그러므로 주응력은 아래와 같이 쉽게 구해질 수 있다.

${\begin{aligned}\sigma _{1}&=\sigma _{{\mathrm {avg}}}+R\\&=70{\textrm {MPa}}\\\end{aligned}}$

${\begin{aligned}\sigma _{2}&=\sigma _{{\mathrm {avg}}}-R\\&=-30{\textrm {MPa}}\\\end{aligned}}$

$\tau _{{\max ,\min }}=\pm R=\pm 50{\textrm {MPa}}$

주축은 (각도는 아래 그림의 각 BOE를 참고)

${\begin{aligned}2\theta _{\mathrm {p} }=\arctan {\frac {2\tau _{xy}}{\sigma _{x}-\sigma _{y}}}=\arctan {\frac {2*40}{(-10-50)}}=-\arctan {\frac {4}{3}}\end{aligned}}$

$\theta _{{p2}}=-26.565^{\circ }$

참고문헌

https://en.wikipedia.org/wiki/Mohr%27s_circle

'이론' 카테고리의 다른 글

열전달 (heat transfer) (0)	2019.01.11
후크의 법칙 (Hook's law) (1)	2019.01.03
단면 1차 모멘트 (0)	2019.01.02
포아송 비 (Poisson's ratio) (0)	2018.12.27
변위, 속도, 가속도 관계 (2)	2018.12.26

[공학나라] 기계 공학 기술정보

모어의 원 (Mohr's circle)

'이론' 카테고리의 다른 글

+ Recent posts

티스토리툴바