//구글애드센스 20230512 // //구글애드센스 20230512 이상 기체의 단열 변화 :: [공학나라] 기계 공학 기술정보
반응형








이상 기체의 가역 단열 변화 (reversible adiabatic process for an ideal gas)




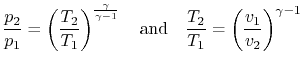
$\displaystyle \frac{p_2}{p_1} = \left(\frac{T_2}{T_1}\right)^{\frac{\gamma}{\ga... ...uad \textrm{and} \quad \frac{T_2}{T_1} =\left(\frac{v_1}{v_2}\right)^{\gamma-1}$


혹은


$\displaystyle pv^\gamma = \textrm{constant, or}$




식의 유도 과정


열역학 1법칙에서 


$ Q=0$, $ du = c_v dT$, $ \textrm{Work} = pdv$ 이므로 

$\displaystyle du + pdv = 0.$-> $\displaystyle \gamma c_v dT = -\gamma pdv$


엔탈피의 정의를 이용하면


$\displaystyle dh = \underline{du + pdv} + vdp.$->$\displaystyle c_p dT = vdp.$

* 밑줄친 부분이 0 이므로



두 식을 연계하면


$\displaystyle -\gamma pdv = vdp\quad \textrm{ or }\quad -\gamma dv/v = dp/p.$ 

적분하면$\displaystyle -\gamma ln(v_2/v_1) = ln(p_2/p_1)\textrm{, or, equivalently,}$$\displaystyle (p_2 v_2^\gamma)/(p_1 v_1^\gamma)=1.$

이상기체 방정식을 적용하면 맨 위의 식이 나온다.






참고문헌


https://web.mit.edu/16.unified/www/FALL/thermodynamics/notes/node18.html









반응형
저작자표시

'이론' 카테고리의 다른 글

열역학 제2법칙 (2nd law of thermodynamics)  (0) 2020.06.23
카르노 싸이클 (Carnot cycle)  (0) 2020.06.16
정적 및 정압 비열  (0) 2020.06.11
열역학 제1법칙 (1st law of thermodynamics)  (0) 2020.06.11
동력학의 기본이론과 질점의 운동학  (0) 2020.05.07

+ Recent posts

티스토리툴바