[공학나라] 기계 공학 기술정보

정적 및 정압 비열 (heat capacity)

열역학의 기본 개념 중 하나.

물질에 열을 가하면 온도가 상승하는데 물질에 따라 온도 상승량이 다르다. 이 때 필요한 열을 나타내는 것이 비열이다. heat capacity를 직역하면 열용량(=비열)이기 때문에 비열이 클수록 1도 올리기 위해 많은 열이 필요하다. 

기체를 다룰 때에는 열을 가하는 과정에 따라 비열이 바뀌게 된다. 예를 들어 열을 가하는 과정에서 부피를 일정하게 한다든지 아니면 압력을 일정하게 한다든지에 따라 비열이 바뀌게 된다.

즉 기체의 비열은 물질뿐만 아니라 열을 가하는 과정에 따라 바뀌게 된다.

정적 비열의 정의

부피를 일정하게 유지하면서 (constant volume), 단위 질량의 물질을 단위 온도만큼 증가시키기 위한 열

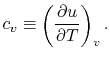
* 열역학 제1법칙의 수식으로 유도하면 위와 같은 수식이 나온다.

* 는 단위 질량에 대한 값이며 는 1 mol에 대한 값으로 표현된다.

정압 비열의 정의

압력을 일정하게 유지하면서 (constant pressure), 단위 질량의 물질을 단위 온도만큼 증가시키기 위한 열

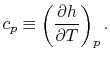
* 열역학 제1법칙의 수식으로 유도하면 위와 같은 수식이 나온다.

* 는 단위 질량에 대한 값이며 는 1 mol에 대한 값으로 표현된다.

이상 기체에서의 정적 및 정압 비열

- 이상 기체에서는 

*, 여기의 기체 상수 R은 아래 일반기체상수를 분자량으로 나눈 값이다.

* 이상 기체의 상태방정식와 열역학 제1법칙을 적절히? 잘 사용하면 위 식이 유도된다.

*  : 일반 기체 상수 (universal gas constant) = 8314 J/(kg K)

-  이상 기체에서는 비열비 (specific heat ratio)  는 항상 1보다 크다.

- 이상 기체에서는 , 는 온도 T 만의 함수이다.

참고문헌

https://web.mit.edu/16.unified/www/FALL/thermodynamics/notes/node18.html

열역학 제1법칙 (1st law of thermodynamics)

"에너지 보존 법칙" 이다. 쉽게 말해 어떤 계(system)의 일하고 남는 열은 내부 에너지로 저장된다는 법칙이다. 참 쉽다.

수식으로 나타내면

 : 계의 내부 에너지 미소 변화량

* 내부 에너지 U는 물체가 가지고 있는 총에너지에서 역학적 및 전기적 에너지를 제외한 에너지를 말한다.

 : 계에 더해진 열에너지 미소 변화량

 : 계가 외부에 한 일 미소 변화량

위 수식을 그대로 이해하면 

"계에 더해진 열에너지"에서 "계가 외부에 한 일"을 빼면 "내부 에너지"의 변화가 된다는 것이다.

예를 들자면 어떤 계에 100 J의 열량이 들어왔는데 10 J의 일을 하면 내부 에너지가 90 J 증가한다는 것이다.

* 미소 변화량은 보통 d 로 표현하는데 Q와 W는 δ로 표현하는 이유

d : 완전 미분 (exact differential) 으로 우리가 보통 알고 있는 바로 그 미분이다. 

δ : 불완전 미분 (inexact differential) 

완전 미분은 상태 1에서 2로 적분할때의 값이 단 하나의 값이지만 불완전 미분은 경로에 따라 그 값이 바뀐다.

즉, 내부 에너지는 상태 1과 2를 알면 적분값이 구해지지만 열량과 일은 상태 1과 2 뿐만 아니라 1에서 2로 가는 경로를 알아야 구해지는 값이다. 쉽게 설명하면 일의 적분값 (일의 총량) 을 구할 때는 1에서 3을 거쳐 2로 갈때와 1에서 2로 바로 갈 때 하는 일이 틀려진다는 의미이다. 더 쉽게 설명하면 불완전 미분인 일의 총 량은 서울에서 부산 갈때 중간에 대전을 거쳐가는지 청주를 거쳐가는지에 따라 하는 일이 틀려진다는 의미이다. 

가역 과정 (reversible process) 에서의 1법칙

가역 과정에서 열역학 제1법칙은 아래와 같이 정의된다.

*가역 과정에 관한 설명은 열역학 제2법칙에 나온다.

*모든 가역 과정은 준정적이지만 모든 준정적 과정은 가역 과정이 아니다. 준정적이래도 마찰 같은 게 있으면 가역 과정이 아니다.

*준정적 과정 (quasi-static process) 이란 변화가 너무 느리다고 가정해서 계가 내부적으로 평행 상태에 있는 것을 말한다. 응? 쉽게 말해 매 순간을 정적 평형상태로 보는 것이다. 응? 쉽게 말해 1에서 2상태로 변할 때 변하는 속도에 영향을 받지 않는다고 가정하는 과정을 말한다.  

혹은

 엔탈피 (entalphy)

* 여기서 엔탈피라는 새로운 개념을 도입하는 데 이는 후에 설명할 개방계에서 계의 경계선을 출입하는 유체의 내부에너지와 일을 합쳐논 개념이다. 일단 그리 알고 가자.

* 위 식의 유도 과정

원래 열역학 1법칙은 아래와 같다.

여기에서 준정적 가정을 더하면 

엔탈피의 미소 변화량은 

위식에 준정적 가정의 열역학 1법칙의 dU를 대입하면

밀폐계와 개방계에서의 열역학 제1법칙

제1법칙은 크게 밀폐계와 개방계로 나누어서 생각하는 경우가 많다.  당연히 물질의 이동이 없는 밀폐계가 개방계보다 이해하기는 더 쉽다.

* 밀폐계 (closed system) 는 쉽게 말해 계의 내외부로 물질의 이동이 없는 경우 (예 : 내연 기관) 이고, 개방계 (open system)은 계의 내외부로 물질의 이동이 있는 경우 (예 : 펌프) 이다. 

준정적 과정에서 둘 다 같은 식 이지만...

밀폐계의 경우는 아래 식이 유리하다.

개방계의 경우는 아래 식이 유리하다.

참고문헌

https://ko.wikipedia.org/wiki/%EC%97%B4%EC%97%AD%ED%95%99_%EC%A0%9C1%EB%B2%95%EC%B9%99

https://web.mit.edu/16.unified/www/FALL/thermodynamics/notes/node17.html

https://www.et.byu.edu/~rowley/ChEn273/Topics/Energy_Balances/Energy_Balance_Closed_Systems/Pressure_Volume_Work.htm

https://en.wikipedia.org/wiki/Quasistatic_process

문제는 https://www.comcbt.com/xe/ny/3770467

문제 / 답

81 / 1

충돌 반발계수를 활용하는 문제로 풀이 시간이 좀 걸림

자동차 A, B, 속도 20 m/s, 반발계수 0.7, 마찰 무시

 공식을 활용하여 X축 및 Y축에 대한 두 식을 만들어 각 방향에 대한 속도를 구하고 합성하면 됨.

(풀이가 김)

충돌 후의 A의 속력은 17.3 m/s

82 / 1

등각가속도 운동에 대한 문제

에서 

각가속도 α = - 80 rad/s / 20 s = - 4 rad/s^2

t = 20 s

ω0 = 80 rad/s

θ0 = 0

을 적용하면

θ = 0.5 x -4 x 20^2 + 80 x 20 = -800 + 1600 = 800 rad = 800 / (2π) = 127 rev (바퀴)

83 / 3

x = X0 sin (ωt) 일 때 가속도를 구하기

변위를 t에 대해 두번 미분하여 구할 수 있음.

변위 

속도 

가속도 

84 / 1

일의 정의에 관한 문제

600 N 사람, 5000 N 엘베, 200 m 케이블

감아올리는데 필요한 일 = 힘 x 거리 = 5600 N x 200 m = 1120000 J = 1120 KJ

85 / 4

대수 감소율 문제 

1자유도 감쇠계 진동 방정식에서 m = 2, c = 3, k = 8 일때 

를 구한후에 

대수감소율식에 적용하면 =2.54

86 / 3

v-t 선도에서 접선의 기울기 = v에 대한 시간 미분 = 가속도

87 / 3

진자의 주기에 관한 문제

달표면 중력 가속도 = 지구표면 중력 가속도 / 6

주기가 T인 단진자를 달로 가져가면 주기는 

지구표면 중력 가속도 

달표면 중력 가속도 

88 / 4

감쇠비가 일정할때 전달률을 1도다 작게 하려면 진동수비의 크기

보다 커야 한다.

89 / 2

3차원 공간에서 각운동량 구하기

L = r x mv

L : 3차원 각운동량 벡터

r : 3차원 (원점에서부터) 위치 벡터

m : 질량 (스칼라)

v : 3차원 속도

x : 외적 (cross product)

* 외적

a = < a1 a2 a3 >

b = < b1 b2 b3 >

a x b = < a2b3 - a3b2, a3b1 - a1b3, a1b2-a2b1 >

r = < a b c >

v = < 0 v 0 >

L = m<-cv 0 av> = mv (-ci + ak)

90 / 2

질량 50 kg 상자, 질량 10 kg 수레, 상자가 넘어지지 않는 힘 P의 최대값

상자가 넘어지지 않는 다는 것 = 상자 왼쪽 아래의 회전 중심에 대해 상자가 회전하지 않는 것 

회전 중심에 대한 모멘트 = 중력에 의한 회전 모멘트 + 가속도에 의한 회전 모멘트 = 0 되는 시점을 찾으면 됨

(시계 방향 모멘트를 +라 가정)

중력에 의한 회전 모멘트 = 회전 중심부터의 거리 x 힘 = 0.4 m x 50 kg x 9.8 = 196 N m

* 힘 P로 밀 때 상자의 가속도 = P / ( 50 + 10 )

가속도에 의한 회전 모멘트 =  - 0.6 m x 50 kg x P / ( 50 + 10 )   

196 = 0.6 m x 50 kg x P / ( 50 + 10 ) 

P = 392 N

질점의 동역학 (뉴튼의 제2법칙)

뉴튼의 운동 제2법칙

F = ma

※ 힘을 가하면 가속도가 발생한다.

질점의 선형 운동량과 각 운동량 (1차원)

선형 운동량 : mv (단위 : kg m/s)

* 질량 x 속도의 개념

각 운동량 : mvr (단위 : kg m2/s)

* 질량 x 속도 x 거리 의 개념

3차원에서 각운동량

3차원에서는 위치벡터와 속도벡터의 외적을 통해 구해진다.

L = r x mv

L : 3차원 각운동량 벡터

r : 3차원 (원점에서부터) 위치 벡터

m : 질량 (스칼라)

v : 3차원 속도

x : 외적 (cross product)

* 외적이 뭔지 까먹었지?

a = < a1 a2 a3 >

b = < b1 b2 b3 >

a x b = < a2b3 - a3b2, a3b1 - a1b3, a1b2-a2b1 >

Staking 조립

두 부품을 억지끼워맞춤으로 조립 혹은 연결하는 과정이다. 일종의 영구적인 체결 방법이다.

예를 들어 A라는 부품에 구멍이 있고 B라는 부품에 보스 (구멍에 끼워 넣는 것) 이 있다고 하면 조립전에 보스는 구멍보다 아주 약간 작게 가공되어 조립은 부드럽게 된다. 이후에 스태킹 (스태이킹?) 펀치라는 도구를 이용해서 보스를 반경 방향으로 넓히고 축방향으로는 압축시켜 억지끼워맞춤을 만들게 된다. 

쉽게 말해 조립후에 연결부품에 변형을 가해 영구적인 체결을 하는 방법이다.

Thermoplastic staking

staking 방법 중의 하나로 heat staking 이라고도 하며 플라스틱으로 된 보스를 열로 변형시켜 억지끼워맞춤 상태로 만들어 영구적인 체결을 하는 것이다.

다양한 분야에 활용되며 빠르고 경제적이고 일관성이 있는 방법이다. 용접은 기본적으로 금속끼리 하는 방법인데 반해 이 방법은 플라스틱과 금속, 플라스틱과 플라스틱 끼리도 가능한 장점이 있으며 리벳이나 나사 같은 부차적인 결합 부품도 필요없다. 

아래 동영상 참고 (50초 부터 보면 된다.)

참고문헌

https://en.wikipedia.org/wiki/Staking_(manufacturing)