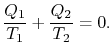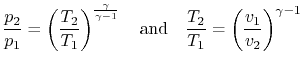//구글애드센스 20230512 // //구글애드센스 20230512 [공학나라] 기계 공학 기술정보 :: [공학나라] 기계 공학 기술정보
반응형







엔트로피 증가량 계산식


이상기체 ($ Pv = RT$)의 등엔트로피 과정의 엔트로피 변화


열역학 1/2법칙과 단열 과정을 가정하면 엔트로피 변화량은 아래와 같이 구해진다.


$\displaystyle \frac{P_2v_2^\gamma}{P_1 v_1^\gamma}=\left[Pv^\gamma\right]^2_1=e^{\Delta s/c_v}.$


위 식에서 가역 과정 ($ \Delta s =0$) 을 가정하면 $ Pv^\gamma = \textrm{constant}$가 된다. 


즉, 단열, 가역과정이 등엔트로피 (isentropic) 과정이다.




두 열원 사이의 열전달 과정의 엔트로피 변화



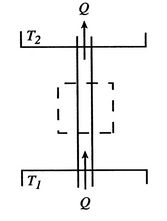
아래 그림과 같이 TH의 열원에서 TL열원으로 Q의 열량이 이동하는 과정에서 (일은 하지 않는다고 가정)


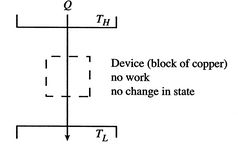
Image fig2tworeservoirs_web


엔트로피 변화량은 TH열원 입장에서는 열이 -, TL 열원 입장에서는 열이 + 이다.


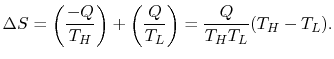
$\displaystyle \Delta S = \left(\frac{-Q}{T_H}\right) + \left(\frac{Q}{T_L}\right) = \frac{Q}{T_H T_L}(T_H-T_L).$



참고 문헌


https://web.mit.edu/16.unified/www/FALL/thermodynamics/notes/node41.html









반응형
저작자표시

'이론' 카테고리의 다른 글

디젤 싸이클 (Diesel cycle)  (0) 2020.06.25
오토 싸이클 (Otto Cycle)  (0) 2020.06.24
열역학 1법칙과 2법칙의 결합 (Gibb's equation)  (0) 2020.06.23
열역학 제2법칙 (2nd law of thermodynamics)  (0) 2020.06.23
카르노 싸이클 (Carnot cycle)  (0) 2020.06.16
반응형






열역학 1법칙과 2법칙의 결합


1법칙과 2법칙 수식을 결합하면 유용한 수식을 만들 수 있다.



1법칙 (항상 가능)


$\displaystyle dU =dQ -dW.$


가역 과정에서 가능한 수식


$\displaystyle dW=PdV,$

$\displaystyle dQ=TdS.$

$\displaystyle dU=dQ-\underline{PdV}, \textrm{ substituted for a reversible }dW$

$\displaystyle dU=\underline{TdS}-dW, \textrm{ substituted for a reversible }dQ.$


1법칙과 2법칙 결합 (항상 가능한 수식, Gibbs 식이라고도 한다)


$\displaystyle du =Tds -Pdv \qquad\textbf{Combined first and second law (a) or Gibbs equation (a).}$


$\displaystyle dh$$\displaystyle =Tds + vdP.$ (엔탈피 형태로 표현)



참고문헌


https://web.mit.edu/16.unified/www/FALL/thermodynamics/notes/node39.html







반응형
저작자표시

'이론' 카테고리의 다른 글

오토 싸이클 (Otto Cycle)  (0) 2020.06.24
엔트로피 증가량 계산식  (0) 2020.06.23
열역학 제2법칙 (2nd law of thermodynamics)  (0) 2020.06.23
카르노 싸이클 (Carnot cycle)  (0) 2020.06.16
이상 기체의 단열 변화  (0) 2020.06.16
반응형






열역학 제2법칙 (2nd law of thermodynamics)


고립된 계의 엔트로피는 감소하지 않는다는 법칙이다. 응? 


우주를 고립계로 보고 결국 우주는 열평형 상태에 다다르고 일을 할 수 있는 에너지가 없어 멸망한다는 우주 멸망 예측의 무시무시한 법칙이다.



서술


열역학 제2법칙은 아래과 같이 설명되는데 모두 같은 얘기다. 읽어보면 너무 당연한 얘기이다.



켈빈-플랑크의 서술


열을 모두 일로 바꾸는 과정은 불가능하다.


* 열효율이 100% 인 뜨거워지지 않는 엔진이 불가능하다.


* 아래 그림과 같은 과정이 불가능하다는 것이다. 즉 열의 일부는 T1 열원으로 가야한다는 것이다.


Image fig2notpossiblekp



클라우지우스의 서술


저온에서 고온으로는 열이 이동하는 것은 불가능하다.


* 아래 그림에서 T1 < T2 일 때, 아래와 같은 과정은 불가능하다.


Image fig2notpossible_web



엔트로피 (entropy)


         열역학 제2법칙에서는 엔트로피라는 새로운 개념이 등장한다. 두둥


엔트로피는 시스템의 열역학적 특성 중의 하나로 가역 과정에서 다음과 같이 정의된다.


$\displaystyle dS = (dQ_\textrm{reversible})/T.$


열역학 제2법칙은 아래와 같이 표현된다. 


$\displaystyle \Delta S_\textrm{total} \geq 0.$


* 가역 과정일 경우에는 0이 된다.



엔트로피의 특성


시스템의 2개의 변수만 알면 구해질 수 있다. 예) $ s = s(T,v)$ 혹은 $ s = s(T,v)$ 혹은 $ s = s(p,v)$


엔트로피 S의 단위는 J/K 이고 단위 질량당 엔트로피 s의 단위는 J/K-kg 이다.



엔트로피 변화량 식 $ dS = dQ_\textrm{rev}/T$에서 Q는 온도가 높은 열원의 열량이며 T는 온도가 낮은 열원의 온도이다.



참고문헌


https://web.mit.edu/16.unified/www/FALL/thermodynamics/notes/node37.html








 

반응형
저작자표시

'이론' 카테고리의 다른 글

엔트로피 증가량 계산식  (0) 2020.06.23
열역학 1법칙과 2법칙의 결합 (Gibb's equation)  (0) 2020.06.23
카르노 싸이클 (Carnot cycle)  (0) 2020.06.16
이상 기체의 단열 변화  (0) 2020.06.16
정적 및 정압 비열  (0) 2020.06.11
반응형






카르노 싸이클 (Carnot cycle)


카르노라는 아저씨가 제안한 이론적인 (이상적인) 싸이클이다.


이 싸이클의 효율은 열역학적 엔진 효율의 최고점이 된다 (=어떠한 엔진도 이보다 효율이 좋을 순 없다).





프로세스


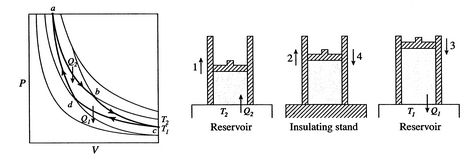
Image fig1CarnotCycle_web

* T2 > T1


4개의 프로세스 (두개의 단열 가역 + 두개의 등온 가역) 로 구성된다.


위 오른쪽 그림은 카르노 싸이클을 열탱크가 붙어있는 피스톤 (내부에는 이상기체) 에 적용한 그림이다. 



a -> b -> c -> d


1. 등온 과정 (온도 T2, Q2 > 0) : a -> b


열탱크로부터 피스톤으로 열 Q2가 전달되는 과정에서 내부 기체의 온도가 일정하게 T2으로 유지되며 압력이 감소하고 부피는 증가하는 과정 



2. 단열 과정 (Q=0) : b (T2) -> c (T1)


열적으로 차단된 상태 (단열) 에서 온도가 낮아지면서 압력이 낮아지고 부피는 팽창하는 과정


(위의 등온 과정과 달리 열이 공급되지 않는 단열 과정이며 온도가 낮아지게 된다.)



3. 등온 과정 (온도 T1, Q1 < 0) : c -> d


열탱크로 열이 유출되는 과정에서 내부 기체의 온도가 일정하게 T1으로 유지되며 압력이 증가하고 부피는 감소하는 과정


(위의 1. 등온 과정의 역과정)



4. 단열 과정 (Q=0) : d (T1) -> a (T2)


열적으로 차단된 상태 (단열) 에서 온도가 높아지면서 압력이 증가하고 부피는 감소하는 과정


(위의 2. 단열 과정의 역과정)




효율


$\displaystyle \eta = 1 - \frac{T_1}{T_2}.\qquad\textbf{Carnot cycle efficiency.}$


* 위 식의 유도 과정


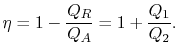열적 효율식 $\displaystyle \eta = 1 - \frac{Q_R}{Q_A}=1+\frac{Q_1}{Q_2}.$ 에서 

$\displaystyle Q_2 = W_{ab} =N\mathbf{R}T_2 [\ln({V_b}/{V_a})],$

$\displaystyle Q_1 = W_{cd} =N\mathbf{R}T_1 [\ln({V_d}/{V_c})] = -N\mathbf{R}T_1 [\ln({V_c}/{V_d})].\quad \textrm{ ($Q_1$ is negative.)}$ 


을 적용하면


$\displaystyle \eta = 1+ \frac{T_1[\ln(V_d /V_c)]}{T_2[\ln(V_b /V_a)]}.$


단열 가역 과정식 $ PV^\gamma= \textrm{constant}$ 혹은 $ T V^{\gamma-1} = \textrm{constant}$를 적용하면 


$\displaystyle \left(\frac{V_d}{V_c}\right)^{\gamma-1} = \frac{(T_2/T_1)}{(T_2/T... ...right)^{\gamma-1},\textrm{ which means that } \frac{V_d}{V_c}=\frac{V_a}{V_b}. $


위의 두 효율식과 위 부피식을 연계하면 $\displaystyle \frac{Q_1}{T_1}+\frac{Q_2}{T_2}= 0.$

결과적으로 위식을 처음 열적 효율식에 대입하면 $\displaystyle \eta = 1 - \frac{T_1}{T_2}.\qquad\textbf{Carnot cycle efficiency.}$



참고문헌



https://web.mit.edu/16.unified/www/FALL/thermodynamics/notes/node24.html



https://en.wikipedia.org/wiki/Carnot_cycle











반응형
저작자표시

'이론' 카테고리의 다른 글

열역학 1법칙과 2법칙의 결합 (Gibb's equation)  (0) 2020.06.23
열역학 제2법칙 (2nd law of thermodynamics)  (0) 2020.06.23
이상 기체의 단열 변화  (0) 2020.06.16
정적 및 정압 비열  (0) 2020.06.11
열역학 제1법칙 (1st law of thermodynamics)  (0) 2020.06.11
반응형








이상 기체의 가역 단열 변화 (reversible adiabatic process for an ideal gas)




$\displaystyle \frac{p_2}{p_1} = \left(\frac{T_2}{T_1}\right)^{\frac{\gamma}{\ga... ...uad \textrm{and} \quad \frac{T_2}{T_1} =\left(\frac{v_1}{v_2}\right)^{\gamma-1}$


혹은


$\displaystyle pv^\gamma = \textrm{constant, or}$




식의 유도 과정


열역학 1법칙에서 


$ Q=0$, $ du = c_v dT$, $ \textrm{Work} = pdv$ 이므로 

$\displaystyle du + pdv = 0.$-> $\displaystyle \gamma c_v dT = -\gamma pdv$


엔탈피의 정의를 이용하면


$\displaystyle dh = \underline{du + pdv} + vdp.$->$\displaystyle c_p dT = vdp.$

* 밑줄친 부분이 0 이므로



두 식을 연계하면


$\displaystyle -\gamma pdv = vdp\quad \textrm{ or }\quad -\gamma dv/v = dp/p.$ 

적분하면$\displaystyle -\gamma ln(v_2/v_1) = ln(p_2/p_1)\textrm{, or, equivalently,}$$\displaystyle (p_2 v_2^\gamma)/(p_1 v_1^\gamma)=1.$

이상기체 방정식을 적용하면 맨 위의 식이 나온다.






참고문헌


https://web.mit.edu/16.unified/www/FALL/thermodynamics/notes/node18.html









반응형
저작자표시

'이론' 카테고리의 다른 글

열역학 제2법칙 (2nd law of thermodynamics)  (0) 2020.06.23
카르노 싸이클 (Carnot cycle)  (0) 2020.06.16
정적 및 정압 비열  (0) 2020.06.11
열역학 제1법칙 (1st law of thermodynamics)  (0) 2020.06.11
동력학의 기본이론과 질점의 운동학  (0) 2020.05.07

+ Recent posts

티스토리툴바